Arithmetic: adding and multiplying¶
Let's consider the following problems you all learned how to solve when you were little kids: adding and multiplying integers. Today we will consider the following questions: given two integers $x,y$ each with $n$ digits, what is the fastest algorithm for adding them? What about multiplying?
Addition¶
1 11 11
18945 18945 18945 18945 18945
23401 23401 23401 23401 23401
_____ _____ _____ _____ _____
6 46 346 2346 42346
# we've already memorized how to add single digits to each other
# additionTable[i][j] gives result of i+j for single digits i, j
additionTable = [
['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'], # 0 + ...
['1', '2', '3', '4', '5', '6', '7', '8', '9', '10'], # 1 + ...
['2', '3', '4', '5', '6', '7', '8', '9', '10', '11'], # 2 + ...
['3', '4', '5', '6', '7', '8', '9', '10', '11', '12'], # 3 + ...
['4', '5', '6', '7', '8', '9', '10', '11', '12', '13'], # 4 + ...
['5', '6', '7', '8', '9', '10', '11', '12', '13', '14'], # 5 + ...
['6', '7', '8', '9', '10', '11', '12', '13', '14', '15'], # 6 + ...
['7', '8', '9', '10', '11', '12', '13', '14', '15', '16'], # 7 + ...
['8', '9', '10', '11', '12', '13', '14', '15', '16', '17'], # 8 + ...
['9', '10', '11', '12', '13', '14', '15', '16', '17', '18'] # 9 + ...
]
# we also memorized how to count from 0 to 19
increment = ['1', '2', '3', '4', '5', '6', '7', '8', '9', '10', '11', '12', '13', '14', '15', '16', '17', '18', '19']
# convert a list of single characters into a string by concatenating them
def listToString(L):
s = ''
for x in L:
s += x
return s
def stripLeadingZeroes(s):
i = 0
while i<len(s) and s[i]=='0':
i += 1
if i == len(s):
return '0'
else:
return s[i:]
# take as input x,y as strings of digits
def add(x, y):
if len(x) < len(y):
x = '0'*(len(y)-len(x)) + x
else:
y = '0'*(len(x)-len(y)) + y
# now both numbers are n digits
# the answer will have either n+1 or n digits
n = len(x)
# we start adding from the rightmost digit
i = n-1
carry = 0
result = ['0']*(n+1)
while i >= 0:
d = additionTable[int(x[i])][int(y[i])]
if carry == 1:
d = increment[int(d)]
result[i+1] = d[len(d)-1]
if len(d) == 2:
carry = 1
else:
carry = 0
i -= 1
if carry == 1:
result[0] = '1'
return listToString(stripLeadingZeroes(result))
add('55', '92')
add('7', '8')
add('14', '3010')
add('23','51')
Runtime analysis: addition¶
How many steps does it take to add $x$ and $y$, each being at most $n$ digits? It scales linearly with $n$. Padding zeroes to make them the same length takes at most $n$ steps. Then the while loop goes on for $n$ steps, and each iteration in the while loop we only do a constant amount of work.
Total time: $O(n)$
Mulitplication¶
123 123 123 123 123
241 241 241 241 241
___ ___ ____ _____ ______
123 123 5043 5043 29643
492 246
multiplicationTable = [ # we memorized x*y for x,y being single digits
['0', '0', '0', '0', '0', '0', '0', '0', '0', '0'],
['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'],
['0', '2', '4', '6', '8', '10', '12', '14', '16', '18'],
['0', '3', '6', '9', '12', '15', '18', '21', '24', '27'],
['0', '4', '8', '12', '16', '20', '24', '28', '32', '36'],
['0', '5', '10', '15', '20', '25', '30', '35', '40', '45'],
['0', '6', '12', '18', '24', '30', '36', '42', '48', '54'],
['0', '7', '14', '21', '28', '35', '42', '49', '56', '63'],
['0', '8', '16', '24', '32', '40', '48', '56', '64', '72'],
['0', '9', '18', '27', '36', '45', '54', '63', '72', '81']
]
# c is a single digit number, and x is arbitrary length. return c*x.
# c and x are strings
def multiplyDigit(c, x):
result = ['0']*(len(x)+1)
carry = '0'
i = len(x)-1
while i >= 0:
d = multiplicationTable[int(c)][int(x[i])]
d = add(d, carry)
result[i+1] = d[len(d)-1]
if len(d) == 2:
carry = d[0]
else:
carry = '0'
i -= 1
return listToString(stripLeadingZeroes(result))
# again x,y are strings of digits
def multiply(x, y):
# make x and y have the same length
if len(x) < len(y):
x = '0'*(len(y)-len(x)) + x
else:
y = '0'*(len(x)-len(y)) + y
n = len(x)
result = '0'
i = n-1
zeroes = ''
while i >= 0:
result = add(result, multiplyDigit(y[i], x) + zeroes)
zeroes += '0'
i -= 1
return result
multiply('11', '12')
multiply('24', '451')
Runtime analysis: multiplication¶
How many steps does it take to multiply $x$ and $y$, each being at most $n$ digits? We do $n$ additions, each time to numbers that are at most $2n$ digits long (since we pad with the zeroes variable, which has at most $n$ zeroes). Each addition thus takes $O(n)$ time.
Total time: $O(n^2)$
Strange situation $\ldots$¶
Addition and multiplication are both basic arithmetic operations, but one takes $\approx n$ steps while the other takes $\approx n^2$. Maybe we are just using the wrong algorithm? After all, these aren't the only algorithms for addition and multiplication.
For example: for addition, we could add $x+y$ by incrementing $x$ repeatedly, $y$ times. The running time would then be $O(y)$. Unfortunately if $y$ is $n$ digits, it could be as big as $10^n-1$ ($n$ $9$'s in a row), so this running time, in terms of $n$, could be as bad as $\approx 10^n$, which is $\gg n$. So the grade school algorithm is better than this naive algorithm of repeated increments. Maybe there's something smarter for multiplication than the grade school algorithm?
The story goes that Andrey Kolmogorov, a giant of probability theory and other areas of mathematics, had a conjecture from 1956 stating that it is impossible to multiply two $n$-digit numbers much faster than $n^2$ time. In 1960, Kolmogorov told many mathematicians his conjecture at a seminar at Moscow State University, and Karatsuba, then in the audience, went home and disproved Kolmogorov’s conjecture in exactly one week 1. Let’s now cover the method he came up with.
The basic idea is something called divide-and-conquer, which we also saw with MergeSort.
Suppose we want to multiply $x$ and $y$. Let's look at a concrete example.
44729013 x 10022889
Here $x = 44729013, y = 10022889$. We begin by splitting the digits in half and writing
$x = 4472\times 10^4 + 9013 = x_{hi}\times 10^4 + x_{lo}$,
$y = 1002\times 10^4 + 2889 = y_{hi}\times 10^4 + y_{lo}$
Then
$x\cdot y = (x_{hi}\times 10^4 + x_{lo})\times (y_{hi}\times 10^4 + y_{lo}) = x_{hi}y_{hi} 10^8 + (x_{hi}y_{lo} + x_{lo}y_{hi})10^4 + x_{lo}y_{lo}$
In other words, to multiply one pair of $8$ digit numbers $x$ and $y$, we just need to multiply four pairs of $4$-digit numbers: $x_{hi}y_{hi}$, $x_{hi}y_{lo}$, $x_{lo}y_{hi}$, $x_{lo}y_{lo}$. This gives us a recursive algorithm! The base case is when the number of digits is $1$, and then we can just use our multiplicationTable.
def multiplyRecursive(x, y):
# let's first make sure both x,y have the same number of digits,
n = max(len(x), len(y))
x = '0'*(n-len(x)) + x
y = '0'*(n-len(y)) + y
if n == 1:
return multiplicationTable[int(x)][int(y)]
xlo = x[n//2:]
ylo = y[n//2:]
xhi = x[:n//2]
yhi = y[:n//2]
A = multiplyRecursive(xhi, yhi)
B = multiplyRecursive(xlo, ylo)
C = multiplyRecursive(xhi, ylo)
D = multiplyRecursive(xlo, yhi)
result = A + '0'*(2*len(xlo))
result = add(result, add(C, D)+'0'*len(xlo))
result = add(result, B)
return result
# sanity check
print(multiplyRecursive('11', '12') == multiply('11', '12'))
print(multiplyRecursive('24', '451') == multiply('24', '451'))
Runtime analysis: recursive multiplication¶
We can analyze what is called a recurrence relation. Let $T(n)$ be the total number of steps to multiply two $n$-digit numbers using the function multiplyRecursive. Then $T(1) = 1$ (since we just look answer up in a table), and otherwise
$T(n) = 4 T(n/2) + O(n)$
Let us assume here that $n$ is a perfect power of $2$, so as we keep dividing by $2$ we are always left with an integer; this just makes our lives easier (but it turns out the same kind of analysis holds in general).
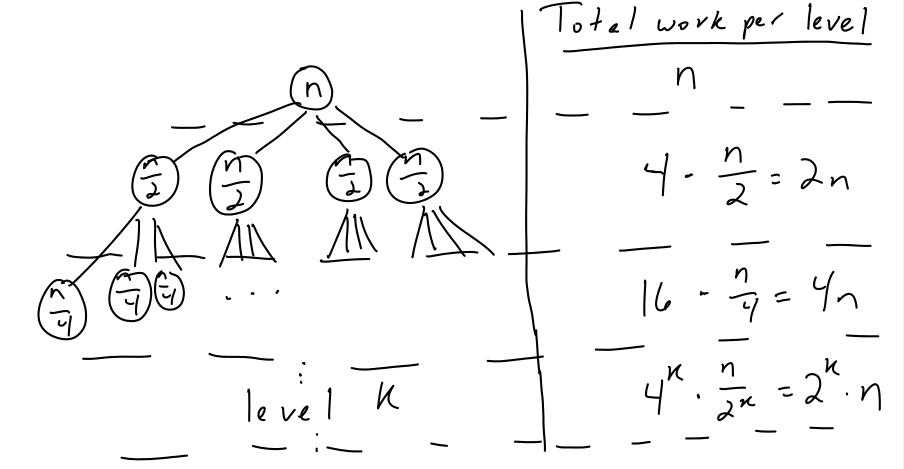
Total work across all levels: $n + 2n + 4n + \ldots + 2^L n$ where $L$ is the number of levels of this recursion tree before we get to the base case of $1$ digit. What is $L$?
$L$ is such that $n/2^L = 1$, so $L = \log_2 n$. Thus the running time is
$n (2^0 + 2^1 + \ldots + 2^{\log_2 n}) = n (2n - 1) = 2n^2 - n$
Total time: $O(n^2)$
Karatsuba's ingenius idea¶
Save on multiplications: instead of $4$ recursive calls, only have $3$! The key insight is that the three values we actually need are:
$A = x_{hi} y_{hi}$
$B = x_{lo} y_{lo}$
and
$Z = x_{lo}y_{hi} + x_{hi} y_{lo}$
We obtained $A$ and $B$ directly, and we naively calculated $Z$ using two recursive multiplication calls, for a total of four calls. How can we get away with three calls? The trick is to define
$E = (x_{lo} + x_{hi}) \times (y_{lo} + y_{hi})$.
Then we can obtain $Z$ as $E - A - B$. Thus we only need to do three recursive calls, and some extra subtractions, but subtractions are as cheap as additions! (only $O(n)$ time)
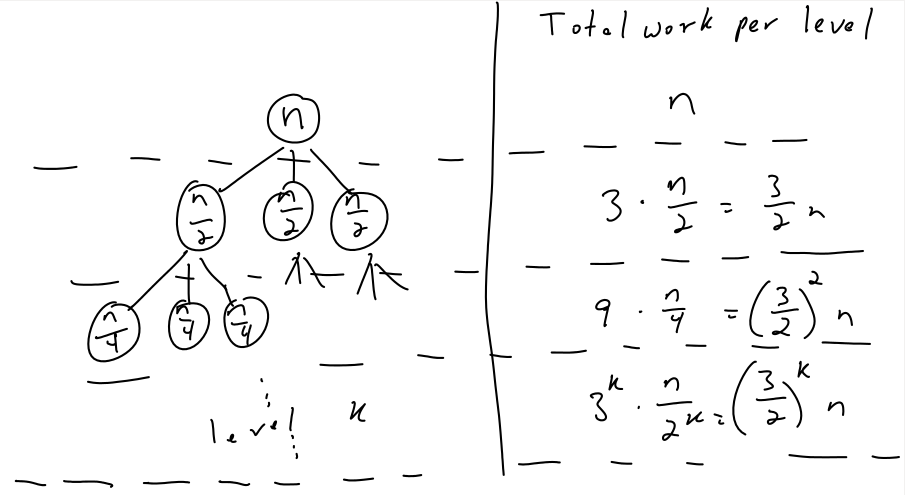
Total work across all levels: $n + \frac 32 n + (\frac 32)^2 n + \ldots + (\frac 32)^L n$ where $L$ is the number of levels of this recursion tree before we get to the base case of $1$ digit. What is $L$ now?
$L$ didn't change, since we still divide $n$ by $2$ at each recursive level! So $L$ is still such that $n/2^L = 1$, so $L = \log_2 n$. Thus the running time is $n \cdot \sum_{k=0}^{\log_2 n} (\frac 32)^k = n \cdot \left(\frac{(\frac 32)^{\log_2 n} - 1}{\frac 12}\right)$
Now, for some arithmetic $\ldots$
$(\frac 32)^{\log_2 n} = (2^{\log_2 \frac 32})^{\log_2 n} = (2^{\log_2 n})^{\log_2 \frac 32} = n^{\log_2 \frac 32} = n^{(\log_2 3) - (\log_2 2)} = n^{(\log_2 3) - 1}$
Therefore $n \cdot \left(\frac{(\frac 32)^{\log_2 n} - 1}{\frac 12}\right) = n \cdot \frac{n^{(\log_2 3) - 1} - 1}{\frac 12} = 2n^{\log_2 3} - 2n$.
Total time: $O(n^{\log_2 3}) = O(n^{1.585\ldots})$
# doing subtraction by hand is similar to addition. we'll leave doing it from scratch as an exercise for you, and
# here we will just "cheat" and use Python's built-in subtraction
def subtract(x, y):
return str(int(x) - int(y))
def karatsuba(x, y):
n = max(len(x), len(y))
x = '0'*(n-len(x)) + x
y = '0'*(n-len(y)) + y
if n == 1:
return multiplicationTable[int(x)][int(y)]
xlo = x[n//2:]
ylo = y[n//2:]
xhi = x[:n//2]
yhi = y[:n//2]
A = karatsuba(xhi, yhi)
B = karatsuba(xlo, ylo)
E = karatsuba(add(xlo, xhi), add(ylo, yhi))
result = A + '0'*(2*len(xlo))
result = add(result, subtract(E, add(A, B))+'0'*len(xlo))
result = add(result, B)
return result
print(karatsuba('11', '12') == multiply('11', '12'))
print(karatsuba('24', '451') == multiply('24', '451'))