Week 3 Day 4 Morning - Graphs¶

%run "boaz_utils.ipynb"

Graphs¶

Often in computation we have data from the world, and a question we want to answer about these data.

To do so, we need to find a model for the data, and a way to translate our question into a mathematical question about the model

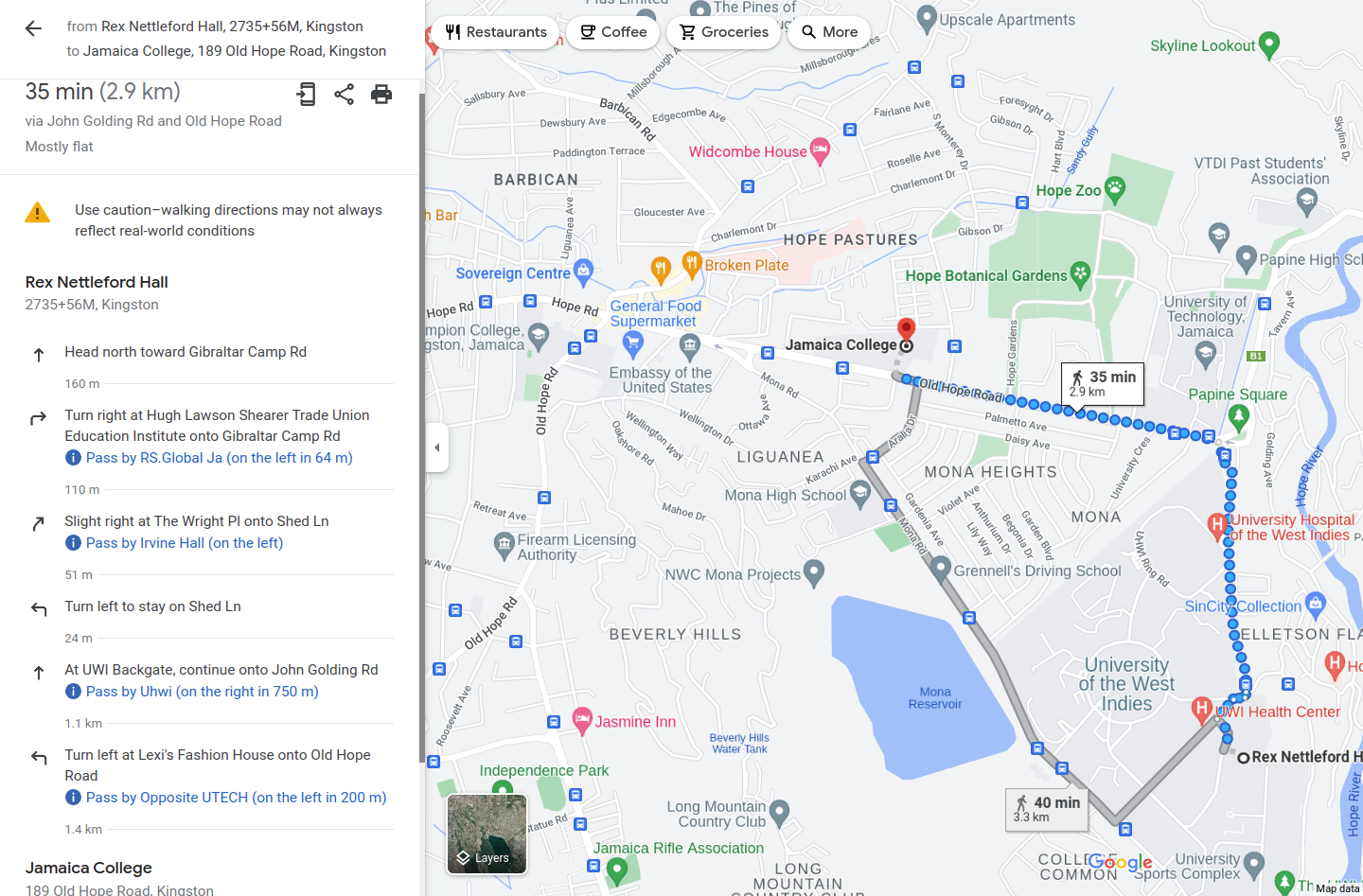
Have map of Kingston, want to find fastest way to get from Rex Nettleford to Jamaica College.
Instagram is trying to figure out how many followers of followers the average Jamaican has.
Geneticist is trying to find which genes relate to a certain colon cancer.

title

What is perhaps most surprising is that these and any many other questions, all use the same mathematical model of a graph

A graph is just a way to store connections between pairs of entities:

The graph of Kingston's roads could be composed of all street intersections, with a connection between intersection $u$ and intersection $v$ if they are directly connected by a road.

The Instagram graph is composed of all Instagram users, with a connection from user $u$ to user $v$ if $u$ follows $v$ .

The gene-symptom interaction graph is composed of all genes and all "symptoms" (also known as phenotypes: some observable differences in people), where gene $u$ is connected to symptom $v$ if there is a correlation between people having the gene $u$ and symptom $v$ .

Mathematically, a graph is a set $V$ of vertices and a set $E$ of pairs of these vertices which is known as the set of edges. We say that a vertex $u \in V$ is connected to $v \in V$ if the pair $(u, v)$ is in $E$ .

A graph where $(u, v)$ is an edge if and only if $(v, u)$ is also an edge is known as an undirected graph. Undirected graphs form an important special case. Otherwise if this is not promised to be the case, we say the graph is directed.

Sometimes the edges (or vertices) of the graph are labeled by a number, which we call a weight. For example in the case of the road network, we might label every road segment with the length of that segment in kilometers.

There are two main representations for graphs. We can always assume the vertices are simply identified by the numbers $0$ to $n - 1$ for some $n$ .

The adjacency list representation is an array $L$ where $L [i]$ is the list of all neighbors of the vertex $i$ (i.e., all $j$ such that $(i, j) \in E$ )

The adjacency matrix representation is an $n \times n$ two-dimensional array $M$ (i.e., matrix) such that $M [i] [j]$ equals $1$ if $j$ is a neighbor of $i$ and equals $0$ otherwise.

# adjacency list representation, G is a list of lists
# G[i] is a list of all vertices i is connected to
for j in G[1]:
    if j==7:
        return True
return False

Questions¶

If a graph has $n$ vertices and $m$ edges - how big is its adjacency list representation? how big is its adjacency matrix representation?

Given a graph $G$ on $n$ vertices and two vertices $i, j$ , how long can it take us (in the worst case) to find out if $j$ is a neighbor of $i$ when $G$ is represented in the adjacency list form? How long will it take in the adjacency matrix form?

Examples:¶

G = [[1],[2],[3],[0]]
draw_graph(G)

G = [[3,1],[0,2],[1,3],[2,0]]
draw_graph(G)

G = [[1,2,3,4,5,6],[0],[0],[0],[0],[0],[0]]
draw_graph(G)

n = 20
cycle = [ [(i+1) % n, (i-1) % n] for i in range(n) ]
draw_graph(cycle)

def grid_neighbors(i,j,n):
    if i==n-1 and j== n-1: return []
    if i==n-1:
        return [i*n+j+1]
    if j==n-1:
        return [(i+1)*n+j]
    return [n*i+((j+1) % n), n*((i+1) % n)+j]

n = 5
grid = [ grid_neighbors(i,j,n) for i in range(n) for j in range(n)  ]

draw_graph(grid,'grid_layout')

Basic graph functions¶

def neighbors(G,u):
    return G[u]

def isedge(G,u,v):
    for i in G[u]:
        if i == v:
            return True
    return False

def vertices(G):
    return len(G)

def addedge(G,i,j):
    if not isedge(G, i, j):
        G[i].append(j)
        
def emptygraph(n):
    G = []
    for i in range(n):
        G.append([])
    return G

neighbors(cycle,0)

isedge(cycle,4,7)

vertices(cycle)

def zeros(n): return [0 for i in range(n)]
def printmatrix(M):
    for L in M:
        print(L)
        
def list2matrix(G):
    n = len(vertices(G))
    M = [zeros(n) for i in range(n)]
    for i in range(n):
        for j in range(n):
            if isedge(G,i,j):
                M[i][j] = 1
            else:
                M[i][j] = 0
    return M

Question: Write function list2matrix(G) that convertes a graph G in adj list format to adj matrix format where M[i][j] equals 1/0 based on whether i is neighbor of j

G = [[3,1],[0,2],[1,3],[2,0]]
M = list2matrix(G)
printmatrix(M)

def list2matrix(G):
    n = len(vertices(G))
    M = [[0 for i in range(n)] for j in range(n)]
    for i in vertices(G):
        for j in vertices(G):
            if isedge(G,i,j):
                (M[i])[j]=1
    return M
G = [[1,4],[0,2],[1,3],[2,4],[3,0]]
printmatrix(list2matrix(G))

Example: Make graph undirected¶

Exercise: Write a function undir that takes a graph G and outputs a graph _G that such that for every i,j the edge i->j is in G if and only if both j->i and i->j are in _G.

def undir(G):
    _G = [[] for i in vertices(G)]
    for i in vertices(G):
        for j in neighbors(G,i):
            addedge(_G,i,j)
            addedge(_G,j,i)
    return _G

G = [[1],[2],[0]]
undir(G)

draw_graph(undir(G))